courses:circuit_analysis:lianxi_04
电路分析·第4章练习
- 正弦量的三要素是(幅值)(角频率)(初相位)。
- 设正弦电压和电流分别为 $u(t)=U\cos(100 t + 45^{\circ})$ 和 $i(t)=I\cos(100 t + 60^{\circ})$,则电压和电流的相位差为 ($-15^{\circ}$),并且电压(滞后)于电流。
- 设正弦电压和电流分别为 $u(t)=U\cos(100 t + 45^{\circ})$ 和 $i(t)=I\cos(100 t + 15^{\circ})$,则电压和电流的相位差为 ($30^{\circ}$),并且电压(超前)于电流。
- 两个同频正弦量的特殊相位关系包括:(同相),其相位差为($0^{\circ}$);(反相),其相位差为($\pm 180^{\circ}$);(正交),其相位差为($\pm90^{\circ}$)。
- 设某正弦电流的幅值为 $14.14\,\mathrm{mA}$,则其有效值为($10\,\mathrm{mA}$); 设某正弦电压的有效值为 $24\,\mathrm{V}$,则其幅值为($34\,\mathrm{V}$)。
- 已知某复数的代数形式为 $F=10 + \mathrm{j}10$,则其三角函数形式为($10\sqrt{2}(\cos45^{\circ}+\mathrm{j}\sin45^{\circ})$),指数形式为($10\sqrt{2}\mathrm{e}^{\mathrm{j}45^{\circ}})$),极坐标形式为($10\sqrt{2}\angle 45^{\circ}$)。该复数的幅值为($10\sqrt{2}$),相位角为($45^{\circ}$)。
- 根据旋转因子 $\mathrm{e}^{\mathrm{j}\theta}$ 可知,任意复数乘以 $\mathrm{j}$ 表示逆时针旋转($90^{\circ}$),乘以 $-\mathrm{j}$ 表示顺时针旋转($90^{\circ}$),乘以 $-1$ 表示顺时针或者逆时针旋转 ($180^{\circ}$)。
- 相量方法是将正弦量的幅值或者有效值作为相量的(模),将正弦量的初相位作为相量的(辐角)。
- 电压 $u(t)=20\sqrt{2}\cos(2t+20^{\circ})$ 的有效值相量表示为($\dot{U}=20\angle20^{\circ}$),幅值相量表示为($\dot{U}=20\sqrt{2}\angle20^{\circ}$)。
- 电阻 VCR 的相量形式为($\dot{U}_R = R\cdot\dot{I}_R$),电阻支路的电压相位和电流相位(相同)。
- 电感 VCR 的相量形式为($\dot{U}_L = \mathrm{j}\omega L\cdot\dot{I}_L$),电感支路的电压相位比电流相位(超前 $90^{\circ}$)。
- 电容 VCR 的相量形式为($\dot{I}_C = \mathrm{j}\omega C\cdot\dot{U}_C$),电容支路的电压相位比电流相位(滞后 $90^{\circ}$)。
- 电抗分为感抗和容抗两种,感抗表达式为($X_L=\omega L$),容抗表达式为($X_C=-\dfrac{1}{\omega C}$)。
- 电纳分为感纳和容纳两种,感纳表达式为($B_L=-\dfrac{1}{\omega L}$),容抗表达式为($B_C=\omega C$)。
- 已知某一端口网络的电压相量 $\dot{U} = U\angle \phi_u$,电流相量 $\dot{I} = I\angle \phi_i$,则该一端口网络的阻抗表达式为($Z=\dfrac{\dot{U}}{\dot{I}}$),阻抗模为($|Z|=\dfrac{U}{I}$),阻抗辐角为($\varphi_Z=\phi_u - \phi_i$)。
- 已知某一端口网络的阻抗为 $Z=3+\mathrm{j}5a$,则当 $a=1$ 时该一端口网络呈(感性),当 $a=-2$ 时该一端口网络呈(容性)。
- 在同一个线性无源一端口网络中,设阻抗为 $Z$、导纳为 $Y$,则满足 $ZY = $($1$),$|Z|\cdot |Y| = $($1$),$\varphi_Z + \varphi_Y = $($0$)。
- 电阻的阻抗表达式为($Z_R = R$),导纳表达式为($Y_R = \dfrac{1}{R}$)。
- 电感的阻抗表达式为($Z_L = \mathrm{j}\omega L$),导纳表达式为($Y_L = \dfrac{1}{\mathrm{j}\omega L}$)。
- 电容的阻抗表达式为($Z_C = \dfrac{1}{\mathrm{j}\omega C}$),导纳表达式为($Y_C = \mathrm{j}\omega C$)。
- 功率因数角($\varphi = \phi_u - \phi_i$),功率因数($\lambda = \cos\varphi$),有功功率($P=UI\cos\varphi$),无功功率($Q=UI\sin\varphi$),视在功率($S=UI$)。
- 在正弦稳态电路中,已知某 RL 串联电路的端电压为 $U$,电阻电压为 $U_R$,则电感电压为($U_L = \sqrt{U^2-U_R^2}$)。
- 在正弦稳态电路中,已知某 RL 并联电路的电阻电流为 $I_R$,电感电流为 $I_L$,则端电流为($I = \sqrt{I_R^2 + I_L^2}$)。
- 已知某无源一端口网络的电压为 $u(t)=100\sqrt{2}\cos(10t+60^{\circ})\,\mathrm{V}$,电流为 $i(t)=2\cos(10t+15^{\circ})\,\mathrm{A}$,则该网络的有功功率为($100\,\mathrm{W}$),无功功率为($100\,\mathrm{var}$),视在功率为($141\,\mathrm{V\cdot A}$),功率因数角为($45^{\circ}$),功率因数为($0.707$)。
- 电阻的(无功)功率为零,电容和电感的(有功)功率为零。
- 在电力系统的输电过程中,应该提高传输的(电压)和(功率因数)。
- 在具有感性负载的网络中,提供功率因数的措施可以是(在负载两端并联电容)。
- 运用相量法分析正弦稳态电路,参考:作业、习题、例题。
- 正弦稳态电路最大功率传输定理的运用,参考:作业、习题、例题。
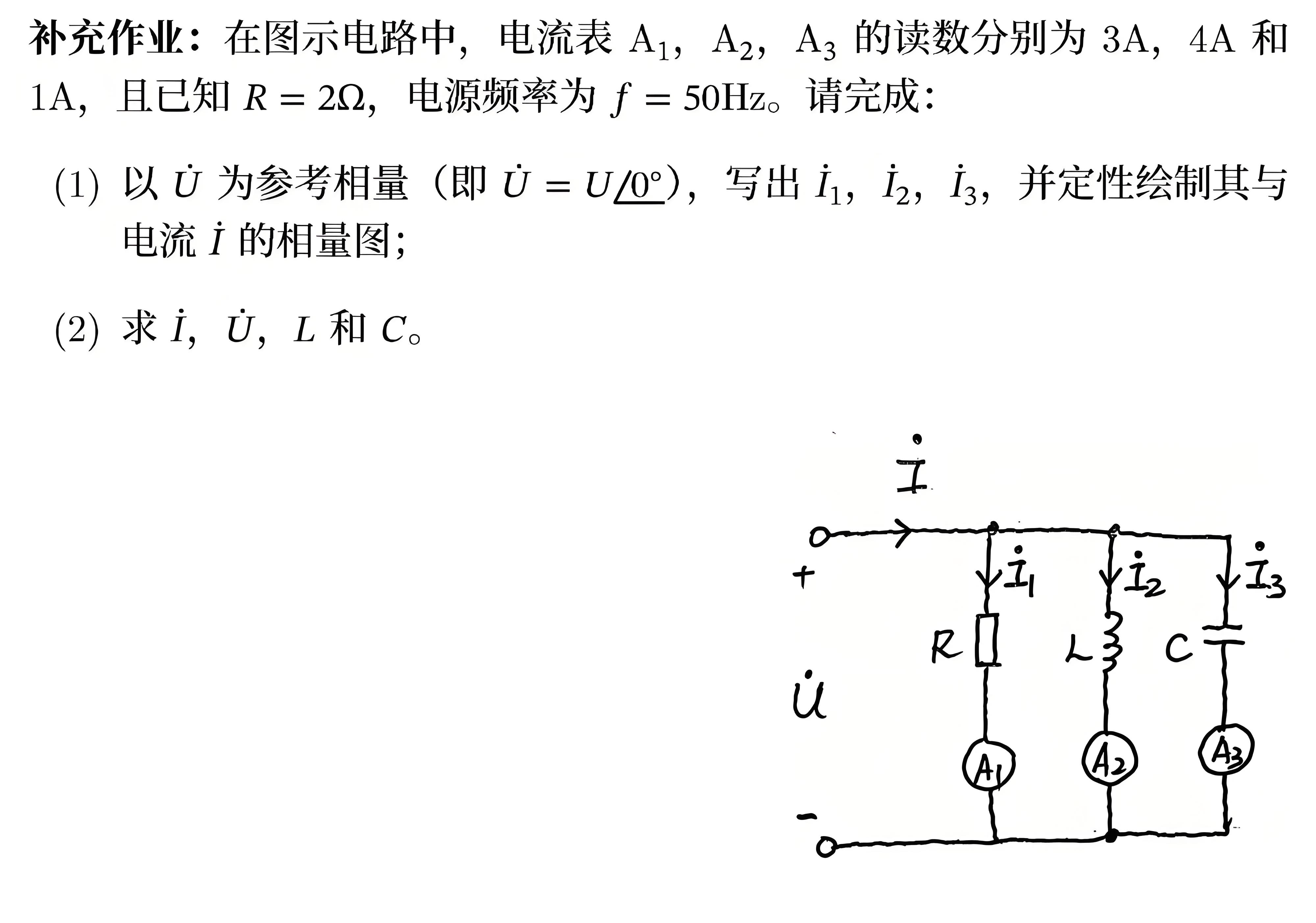
补充作业: